[Coding029] 图 - 最短路径

Dijkstra算法 - 迪杰斯特拉算法

More coding records

Get the knowledge flowing and circulating! :)

目录

标题：Dijkstra算法

概念

迪杰斯特拉算法（英语：Dijkstra's algorithm），又称戴克斯特拉算法。是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发现的算法。Dijkstra算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。

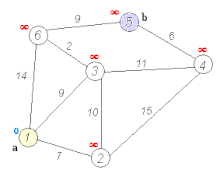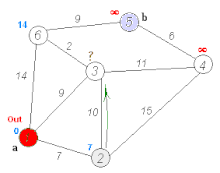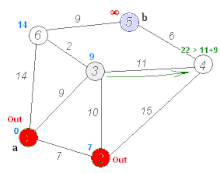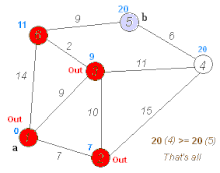
戴克斯特拉算法运行演示（找到a，b之间的最短路）
本算法每次取出未访问结点中距离最小的，用该结点更新其他结点的距离。在演示过程中访问过的结点会被标为红色。

该算法解决了图 $G=⟨V,E⟩$$G=\left \langle V, E \right \rangle$ 上带权的单源最短路径问题。具体来说，Dijkstra算法设置了一顶点集合 $S$$S$ ，在集合 $S$$S$ 中所有的顶点与源点 $s$$s$ 之间的最终最短路径权值均已确定。算法反复选择最短路径估计最小的顶点 $u\in V-S$$u \in V - S$ 并将 $u$$u$ 加入 $S$$S$ 中。该算法常用于路由算法或者作为其他图算法的一个子模块。

举例来说，如果图中的顶点表示城市，而边上的权重表示城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。

• 应当注意，绝大多数的Dijkstra算法不能有效处理带有负权边的图。

• Dijkstra算法在计算机科学的人工智能等领域也被称为均一开销搜索，并被认为是最良优先搜索的一个特例。

——维基百科

实例

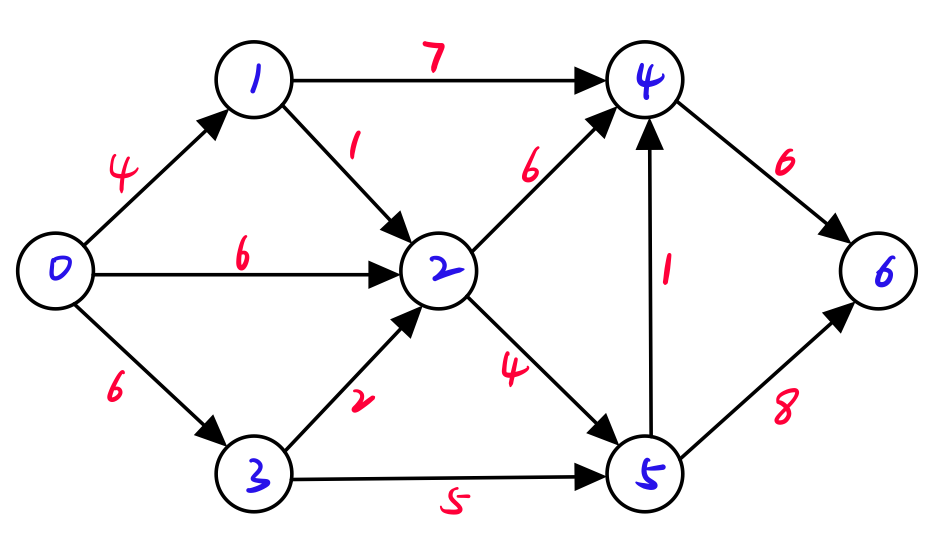
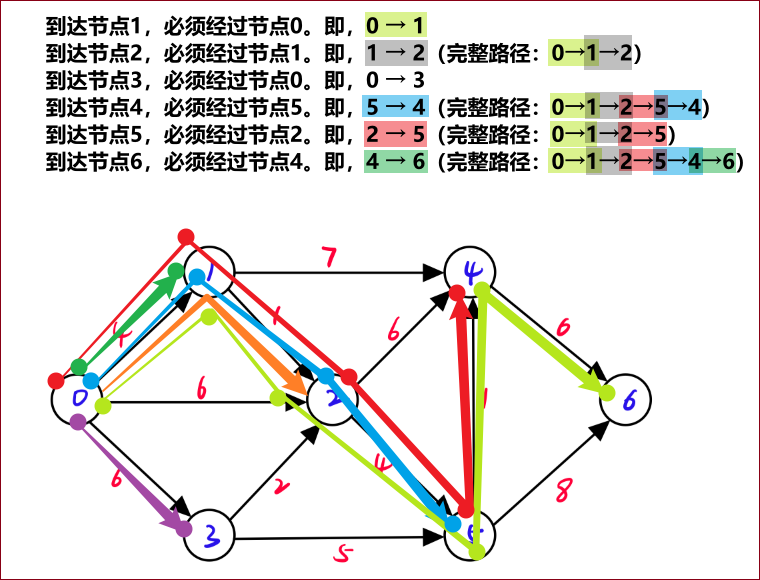
部分代码解读

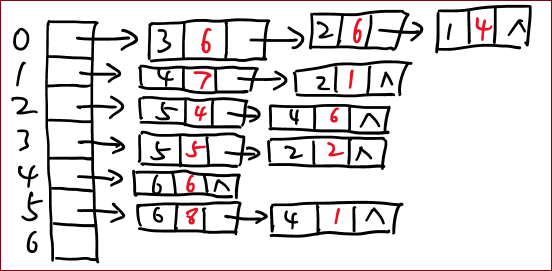
1. 邻接表的建立

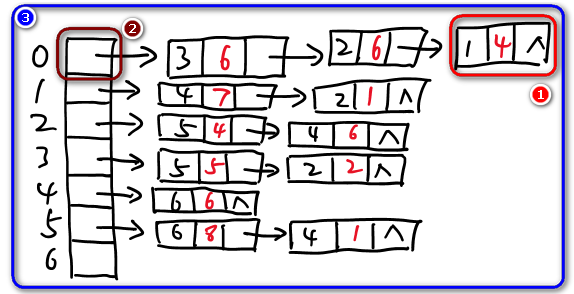
邻接表的组成

• Part❶：边节点；

• Part❷：头节点；

• Part❸：头节点列表；

代码

​x
1
// part01
2
// 邻接表的边结点（ArcNode)  
3
typedef struct ArcNode
4
{
5
    int adjvex;
6
//  char arcInfo;
7
    int arcWeight;
8
    struct ArcNode* nextarc;
9
}ArcNode;
10

11
// part02(part01)
12
// 邻接表的头节点（VNode) 
13
typedef struct VNode
14
{
15
    char vexInfo;
16
    ArcNode* firstArc;
17
}VNode;
18

19
// part03(part02)
20
// 邻接表（包括图的顶点总数、边的总数、头节点列表） 
21
typedef struct ALGraph
22
{
23
    int nums_vertex;
24
    int nums_edge;
25
    int type; // type = 0 表示无向图，type = 1 表示有向图； 
26
    VNode VertexList[100];
27
}ALGraph;

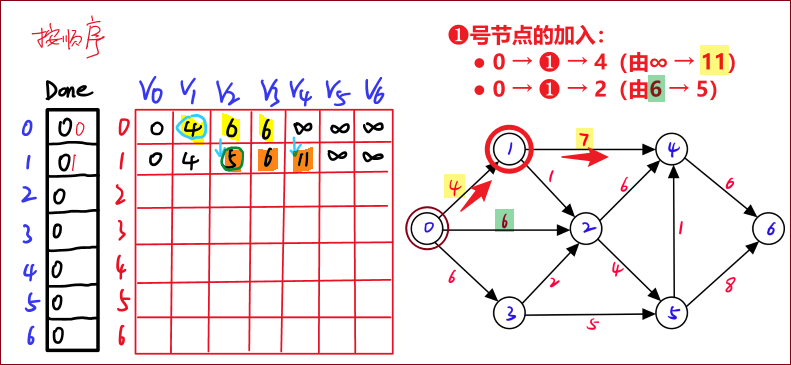
2. 处理每个节点（手绘理解过程）

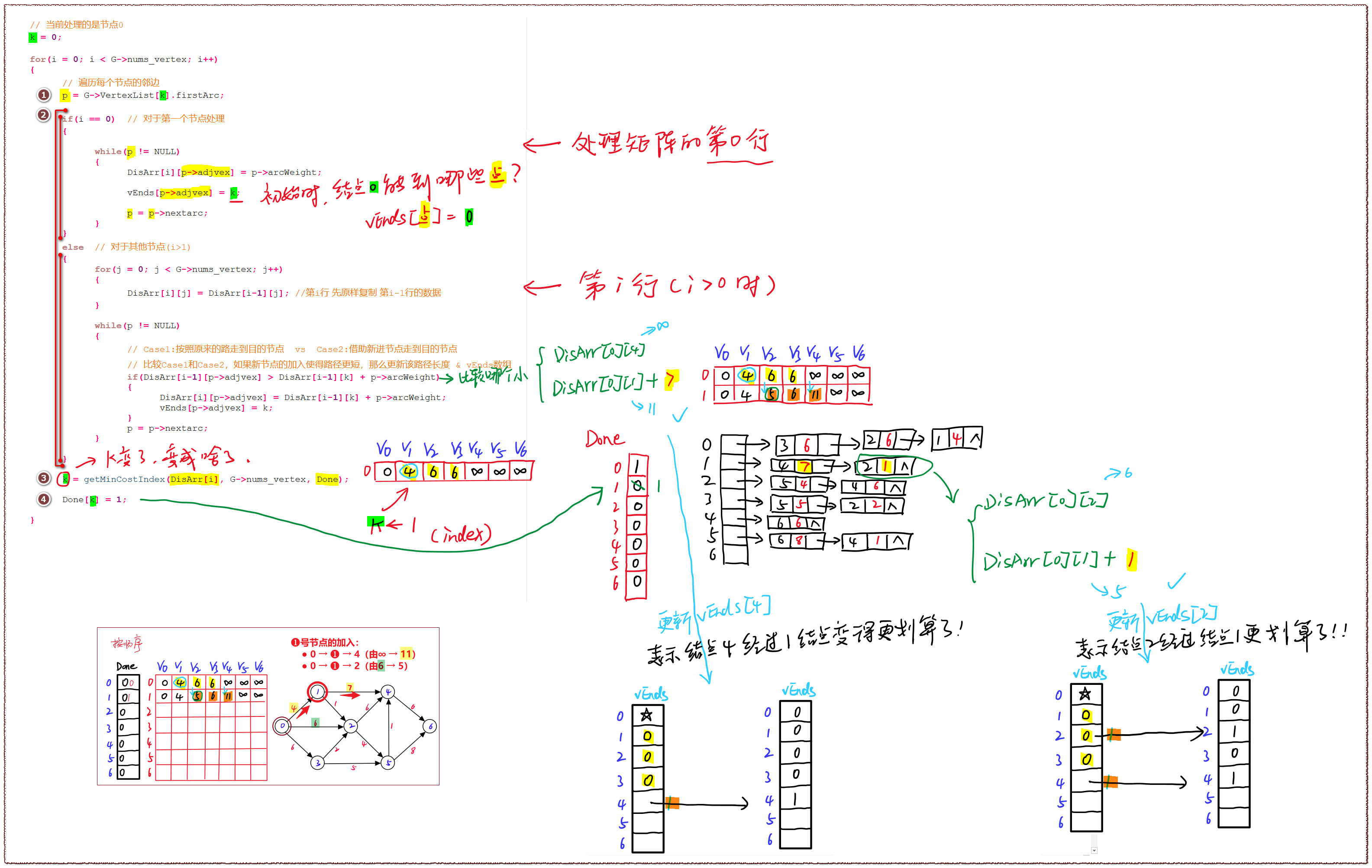
整体执行过程

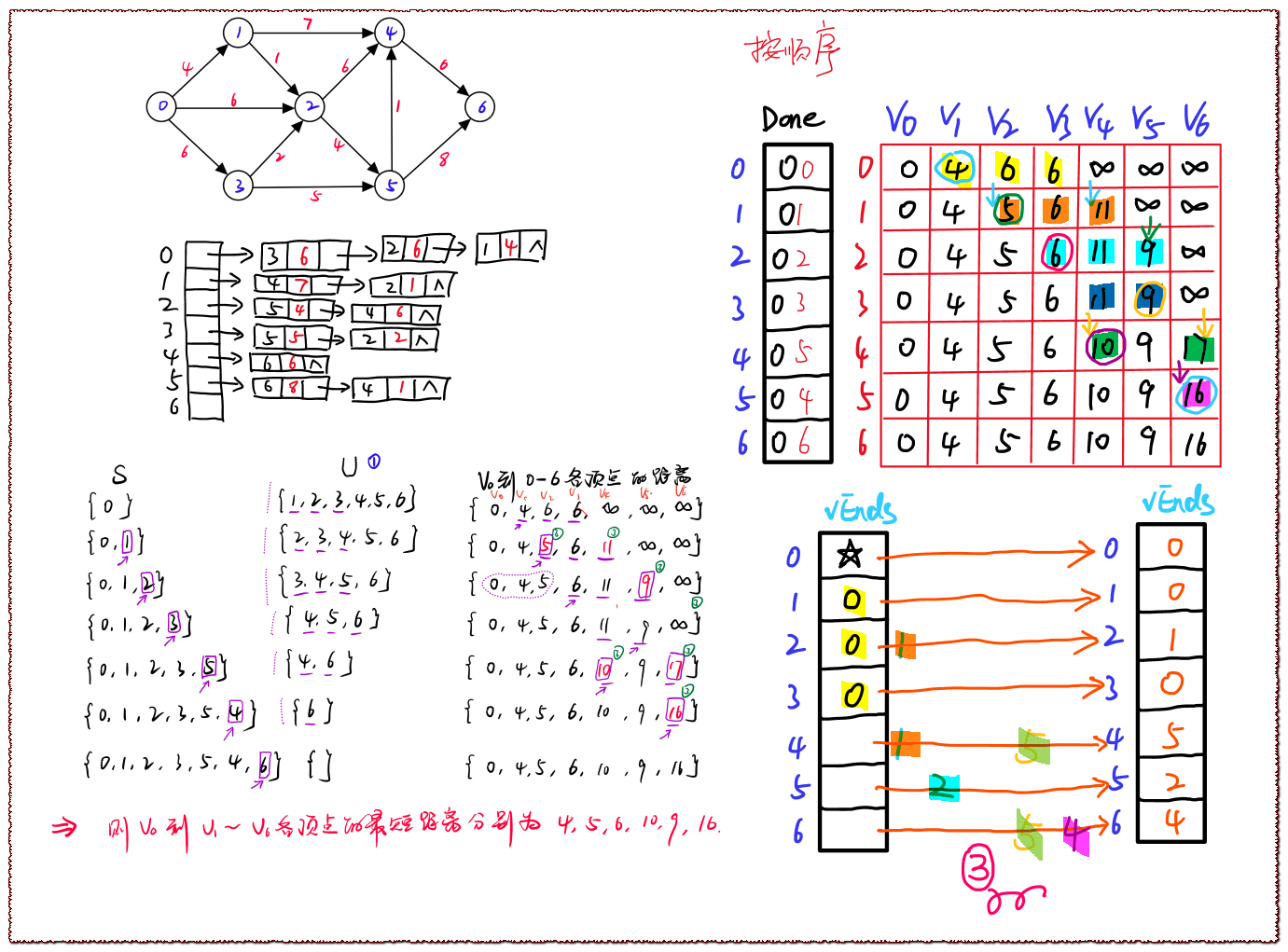
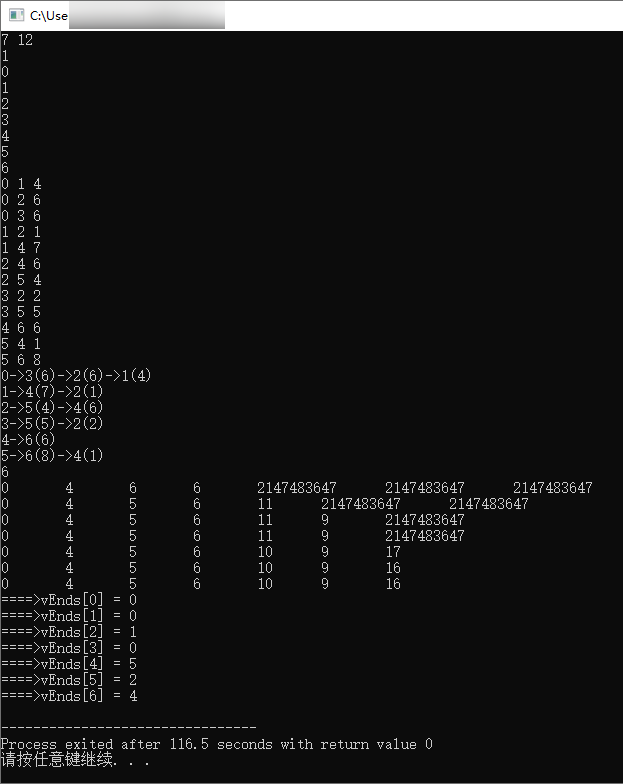
结果的构造

完整代码

x
1
// Dijkstra - 单源最短路径
2

3
#include<stdio.h>
4
#include<stdlib.h>
5
#include<malloc.h>
6

7

8
#define INF    (~(0x1<<31)) 
9

10
// part01
11
// 邻接表的边结点（ArcNode)  
12
typedef struct ArcNode
13
{
14
    int adjvex;
15
//  char arcInfo;
16
    int arcWeight;
17
    struct ArcNode* nextarc;
18
}ArcNode;
19

20
// part02(part01)
21
// 邻接表的头节点（VNode) 
22
typedef struct VNode
23
{
24
    char vexInfo;
25
    ArcNode* firstArc;
26
}VNode;
27

28
// part03(part02)
29
// 邻接表（包括图的顶点总数、边的总数、头节点列表） 
30
typedef struct ALGraph
31
{
32
    int nums_vertex;
33
    int nums_edge;
34
    int type; // type = 0 表示无向图，type = 1 表示有向图； 
35
    VNode VertexList[100];
36
}ALGraph;
37

38
void CreateALGraph(ALGraph* G)
39
{
40
    scanf("%d%d", &G->nums_vertex, &G->nums_edge);
41
    scanf("%d", &G->type);
42
    getchar(); // 接收回车换行符，不然输入上一行的数字之后的回车换行符，就会被下一次输入的字符获取 
43
    char a;
44
    int i = 0;
45
    for(i = 0; i < G->nums_vertex; i++)
46
    {
47
        scanf("%c", &G->VertexList[i].vexInfo);
48
        G->VertexList[i].firstArc = NULL;
49
        getchar();  // 接收回车换行符，不然输入上一行的数字之后的回车换行符，就会被下一次输入的字符获取 
50
    }
51
        
52
    int start, end;
53
    int arcWeight; 
54
    for(i = 0; i < G->nums_edge; i++)
55
    {
56
        scanf("%d%d%d", &start, &end, &arcWeight);
57
        ArcNode* newNode = (ArcNode*)malloc(sizeof(ArcNode));
58
        if(newNode == NULL) exit(0);
59
        
60
        newNode->adjvex = end;
61
        newNode->arcWeight = arcWeight;
62
        newNode->nextarc = G->VertexList[start].firstArc;
63
        G->VertexList[start].firstArc = newNode;
64
        
65
        if(G->type == 0) // 无向图对称处理即可 
66
        {
67
            ArcNode* otherNode = (ArcNode*)malloc(sizeof(ArcNode));
68
            if(otherNode == NULL) exit(0);
69
            otherNode->adjvex = start;
70
            otherNode->arcWeight = arcWeight;
71
            otherNode->nextarc = G->VertexList[end].firstArc;
72
            G->VertexList[end].firstArc = otherNode;
73
        }
74
    }   
75
}
76

77
void prtALGraph(ALGraph* G)
78
{
79
    int i = 0;
80
    for(i = 0; i < G->nums_vertex; i++)
81
    {
82
        printf("%c", G->VertexList[i].vexInfo);
83
        ArcNode *p = G->VertexList[i].firstArc;
84
        while(p != NULL)
85
        {
86
            printf("->%d(%d)", p->adjvex, p->arcWeight);
87
            p = p->nextarc; 
88
        }
89
        printf("\n"); 
90
    }
91
}  
92

93

94

95
// 获取当前源点到各个目的点的距离中最小的那个（这里参与排序的不包括已经处理过的目的点 - 用Done数组标记） 
96
int getMinCostIndex(int Arr[], int len, int Done[])
97
{
98
    int min = INF;
99
    int i;
100
    int index = 0;
101
    for(i = 0; i < len; i++)
102
    {
103
        if(Arr[i] < min && Done[i] == 0) 
104
        {
105
            min = Arr[i];
106
            index = i;
107
        }
108
    }
109
    return index;
110
}
111

112
void Dijkstra(ALGraph* G)
113
{
114
    // 如果已处理的节点：Done[1] = 1, 表示节点1已经加入到最短路径家庭 
115
    int Done[100] = {0};
116
    
117
    // 新节点加入进来作为数值，其他节点作为索引，即：vEnds[index] = value 
118
    // 用于追溯最短路径的节点序列 
119
    int vEnds[100] = {0};
120

121
    
122
    int i, j;
123
    
124
    // 每次处理的最短边的端点
125
    int k;
126
    
127
    // 初始路径长度矩阵全部置为无穷大，然后再一步步处理（细化） 
128
    int DisArr[100][100];
129
    for(i = 0; i < G->nums_vertex; i++)
130
    {
131
        for(j = 0; j < G->nums_vertex; j++)
132
        {
133
            DisArr[i][j] = INF; 
134
        }
135
    }
136
    
137
    // 节点0加入 
138
    Done[0] = 1;
139
     
140
    vEnds[0] = 0;
141
    
142
    // 节点0到自己的路径长度为0 
143
    DisArr[0][0] = 0;
144
    
145
    ArcNode *p;
146
    
147
    // 当前处理的是节点0 
148
    k = 0;
149

150
    for(i = 0; i < G->nums_vertex; i++)
151
    {
152
        // 遍历每个节点的邻边 
153
        p = G->VertexList[k].firstArc;
154
    
155
        if(i == 0)  // 对于第一个节点处理
156
        {
157
             
158
            while(p != NULL)
159
            {
160
                DisArr[i][p->adjvex] = p->arcWeight;
161
                
162
                vEnds[p->adjvex] = k;
163
                
164
                p = p->nextarc; 
165
            }
166
        }
167
        else  // 对于其他节点(i>1) 
168
        {
169
            for(j = 0; j < G->nums_vertex; j++)
170
            {
171
                DisArr[i][j] = DisArr[i-1][j]; //第i行 先原样复制 第i-1行的数据 
172
            }
173
            
174
            while(p != NULL)
175
            {
176
                // Case1:按照原来的路走到目的节点  vs  Case2:借助新进节点走到目的节点  
177
                // 比较Case1和Case2，如果新节点的加入使得路径更短，那么更新该路径长度 & vEnds数组 
178
                if(DisArr[i-1][p->adjvex] > DisArr[i-1][k] + p->arcWeight)
179
                {
180
                    DisArr[i][p->adjvex] = DisArr[i-1][k] + p->arcWeight;
181
                    vEnds[p->adjvex] = k;
182
                }
183
                p = p->nextarc;
184
            }
185
            
186
        }
187
        
188
        k = getMinCostIndex(DisArr[i], G->nums_vertex, Done);
189
        
190
        Done[k] = 1;
191
        
192
    }
193
    
194
    for(i = 0; i < G->nums_vertex; i++)
195
    {
196
        for(j = 0; j < G->nums_vertex; j++)
197
        {
198
            printf("%d\t", DisArr[i][j]);
199
        }
200
        printf("\n");
201
    }
202
    
203
    for(i = 0; i < G->nums_vertex; i++)
204
    {
205
        printf("====>vEnds[%d] = %d \n", i, vEnds[i]);
206
    }
207

208
} 
209

210

211
int main()
212
{
213
    ALGraph *G = (ALGraph*)malloc(sizeof(ALGraph));
214
    CreateALGraph(G);
215
    prtALGraph(G);
216
    
217
    Dijkstra(G);
218
    
219
    return 0;
220
}
221

222

223
/* 输入: 顶点数 | 边数 | 图的类型（有向or无向） | 顶点的编号 | 边的连接情况和权重
224

225
7 12
226
1
227
0
228
1
229
2
230
3
231
4
232
5
233
6 
234
0 1 4
235
0 2 6
236
0 3 6
237
1 2 1
238
1 4 7
239
2 4 6
240
2 5 4
241
3 2 2
242
3 5 5
243
4 6 6
244
5 4 1
245
5 6 8
246

247
*/
248

249
/* 输出：
250
-----------------
251
0->3(6)->2(6)->1(4)
252
1->4(7)->2(1)
253
2->5(4)->4(6)
254
3->5(5)->2(2)
255
4->6(6)
256
5->6(8)->4(1)
257
6
258
-----------------
259
0       4       6       6       2147483647      2147483647      2147483647
260
0       4       5       6       11      2147483647      2147483647
261
0       4       5       6       11      9       2147483647
262
0       4       5       6       11      9       2147483647
263
0       4       5       6       10      9       17
264
0       4       5       6       10      9       16
265
0       4       5       6       10      9       16
266
====>vEnds[0] = 0
267
====>vEnds[1] = 0
268
====>vEnds[2] = 1
269
====>vEnds[3] = 0
270
====>vEnds[4] = 5
271
====>vEnds[5] = 2
272
====>vEnds[6] = 4
273
*/

line167 ~ line186

运行结果